次に満員電車が感染リスクとなるのかどうかに関して考察を行うにあたり一般的な通勤電車の車両における換気がどのようになっているのかに関するデータをネットで検索したところ鉄道技研がスーパーコンピュータを用いて試算した報告を見つけた(8)。
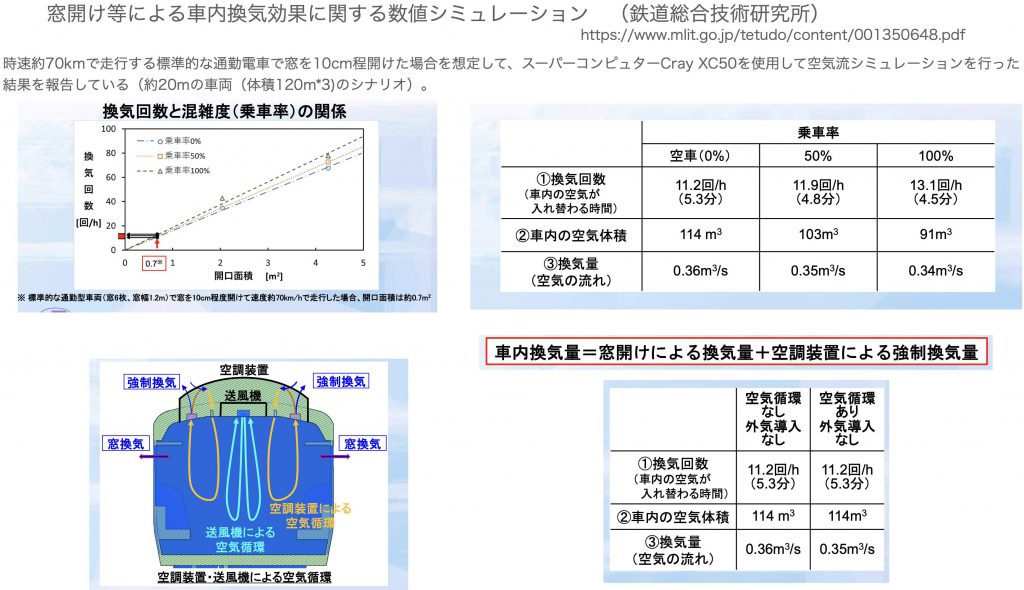
これによると乗車率により窓開けによる換気量(自然換気:natural ventilation)はほぼ影響を受けないとされていた(≒0.35m*3/S)。また、機械的強制換気( mechanical ventilation : =0.43m*3/S )は、窓開けによる換気に影響しないことも試算データからわかっているので車内換気量はこの二つの和(重ね合わせ)となる。このことは換気量Qが定数となる事を示し、Qが定数項ならIpqt/Qは車内に存在する感染者の数(I)とその感染者の放出するERq(q)と暴露時間(t)により大きさが決まり、それに準じた感染確率が決定されることになる。ある一定の低い割合で乗客に感染者が混在するのであれば、乗客が多いほど感染リスクは大きくなるのは自明である。また、偶然感染者が多数同乗していた場合、車両の感染リスクは極めて高いということになる。逆に感染者がいなければ定員オーバーでも感染は成立しない。或る程度(対象地域における感染率で1%以上)市中に蔓延するまでは上述のようなロシアンルーレットまがいの”まだら”感染型のリスクが存在することを認識する必要がある。”電車では感染しない”という逸話はありえず、その他の公共施設と同様に感染リスクが存在する。複数人に接触する場でマスクなしでもCOVID19に感染しない事象は、今までたまたま感染者と同席したことがないか、感染者のERqが最小値でかつ、暴露時間が極端に短いことにより運よく感染を回避できている場合と考えられ地域での感染率が上昇してくるとこのような確率的回避事象は消滅すると考えられる。満員で感染者も複数同乗(平均10~20%)といったシナリオでも感染確率が1%以下に抑えられるような絶対換気量を算出する必要があり、是非ともこの値をクリアできていることを試算して頂きたいと思う。
閉鎖空間での感染リスクを考えるとき、一様な条件が成立するならWells-Rileyの方程式でリスク評価は可能である。しかしながら複数のスペースとの連結や一定のスペース内での空気の拡散状況が大きく異なる場所が存在すると感染リスクの概算は困難となる。
part 3では、呼出された飛沫ベクトルの描く軌跡(ベクトル場)とThermal effect、感染リスクに関して考察してみる。
Uploaded on December 13, 2020.
参考文献
1. Gammaitoni L, Nucci MC. Using a mathematical model to evaluate the efficacy of TB control measures. Emerging Infectious Diseases 1997; 3(3): pp335-342
2. Dai H, Zhao B. Association of the infection probability of COVID-19 with ventilation rates in confined spaces. BUILD SIMUL 2020; 13: pp1321 – pp1327
3. Yu ITS, Li, Y, et al. Evidence of Airborne Transmission of the Severe Acute Respiratory Syndrome Virus. N. Engl. J. Med 2004; 350: pp1731–pp1739
4. Noakes CJ, Sleigh PA, et al. Appraising healthcare ventilation design from combined infection control and energy perspectives. HVAC&R Research; 18 (4): pp658 -pp 670.
5. Morawska L, Johnson GR, et al. Size distribution and sites of origin of droplets expelled from the human respiratory tract during expiratory activities. Aerosol Science 2009;40: pp256 — pp269
6. Buonanno G, Stabile L, et al. Estimation of airborne viral emission: Quanta emission rate of SARS-CoV-2 for infection risk assessment. Environment International 2020; 141: pp1-pp8
7. Noakes CI, Beggs CB, et al. Modelling the transmission of airborne infections in enclosed spaces. Epidemiol Infect 2006; 134: pp1082 – pp1091
8. 窓開け等による車内換気効果に関する数値シミュレーション(試算)(その2). (公財) 鉄道総合技術研究所 2020.10.28 https://www.mlit.go.jp/tetudo/content/001370017.pdf