③一般的な感染症の数理モデル(SEIR)とWells-Rileyの方程式との関係
感染リスクを評価する上で、ある特定スペースの単位時間あたりの換気量、感染性量子の単位時間あたりの放出量、感受性者の単位時間あたりの換気量の関係を表現する時間微分方程式が必要となる。これはSEIRモデルをERqを用いて書き換えを行うことで得られる。以下にその導出過程を示す。

係数比較によりdriving forceである感染伝播係数(感染率)βが、ERqと感受性者の一人当たりの安静時換気量(≒0.01m*3/min)の積に比例し、単位時間あたりの換気数、1回あたりの室内換気量に反比例することが示された。pは定数であり、VAも実際のところ施設ごとに決まってしまう定数項となるので、ERqの値が大きいか、小さいかでバイオエアロゾル感染の脅威の大きさを数値として実感できる。
④ERqから考える特定空間における感染リスクの推定
感染リスクを考えるには、時間tにおける感染性量子の濃度n(t)を導き出す必要があり、これは以下の方程式で表現される。

以上により暴露時間がTであるとき感染確率R(%)はWells-Reillyの方程式にn(t)の時間積分を代入した形で表現できる。

COVID19のERq = 14〜48 q/hとの報告がある(2)。Wells-Rileyの一般方程式に、このERq(= q)を用いて感染確率Pを評価できるが、マスクをすることによる感染性量子のフィルタリング効果を考慮すると以下のように書き換えられる。Q = AV ( A : Air chage per hour (ACH; 換気回数)、VはAC1回分の換気量)。

書き換えした方程式と上述のCOVID-19のERqを用いてDaiら(2)はいろんな公共施設におけるシナリオを想定して、感受性者、感染者の両者がともにマスクをしている場合(Y)とマスクをしていない場合(N)に分けて、集団内に感染者がたった一人存在した場合の感染確率とそれを達成するのに必要な換気回数を算出している(see→Table2)。
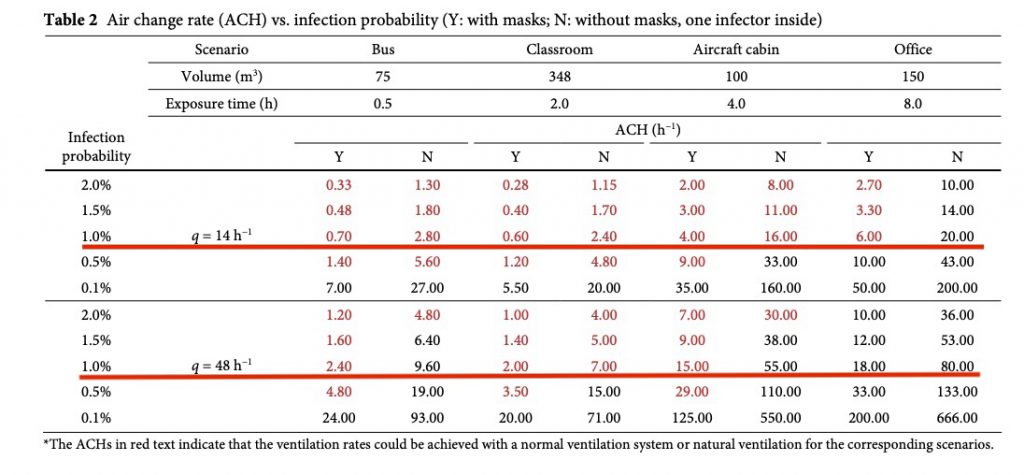
ERqが、最小の14/h、最大の48/hの時感染確率が1%に抑えられる換気回数の行に赤いアンダーラインを引いた。スーパースプレッダーが一人潜在するだけで2倍以上の換気回数が必要となることがわかる。